Seperti yang anda ketahui, sebarang kuantiti fizik tergolong dalam salah satu daripada dua jenis, sama ada skalar atau vektor. Dalam artikel ini, kami akan mempertimbangkan ciri kinematik seperti kelajuan dan pecutan, dan juga menunjukkan ke mana vektor pecutan dan kelajuan diarahkan.
Apakah itu kelajuan dan pecutan?
Kedua-dua kuantiti yang dinyatakan dalam perenggan ini adalah ciri penting bagi sebarang jenis pergerakan, sama ada ia menggerakkan badan dalam garis lurus atau sepanjang laluan melengkung.
Kelajuan ialah kadar perubahan koordinat dari semasa ke semasa. Secara matematik, nilai ini adalah sama dengan terbitan masa bagi jarak yang dilalui, iaitu:
v¯=dl¯/dt.
Di sini vektor l¯ diarahkan dari titik permulaan laluan ke titik akhir.
Sebaliknya, pecutan ialah kelajuan yang mana kelajuan itu sendiri berubah mengikut masa. Dalam bentuk formula, ia boleh ditulis seperti ini:
a¯=dv¯/dt.
Jelas sekali, mengambil terbitan kedua daripadavektor anjakan l¯ dalam masa, kita juga akan mendapat nilai pecutan.
Memandangkan kelajuan diukur dalam meter sesaat, pecutan, mengikut ungkapan bertulis, diukur dalam meter sesaat kuasa dua.

Di manakah vektor pecutan dan halaju?
Dalam fizik, sebarang pergerakan mekanikal badan biasanya dicirikan oleh trajektori tertentu. Yang terakhir ialah beberapa lengkung khayalan di mana badan bergerak di angkasa. Contohnya, garis lurus atau bulatan ialah contoh utama laluan gerakan biasa.
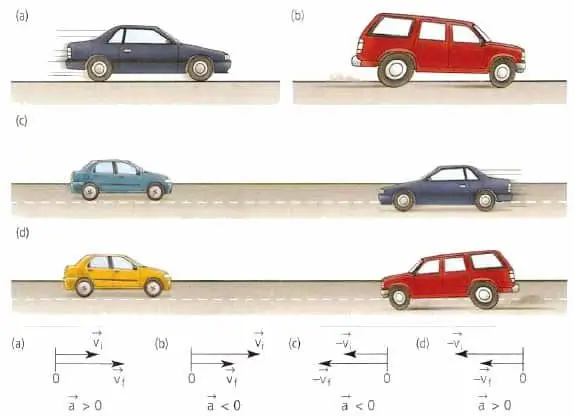
Vektor halaju badan sentiasa diarahkan ke arah pergerakan, tidak kira sama ada badan itu perlahan atau memecut, sama ada ia bergerak dalam garis lurus atau sepanjang lengkung. Bercakap dalam istilah geometri, vektor halaju diarahkan secara tangensial ke titik trajektori di mana jasad itu berada pada masa ini.
Vektor pecutan bahan atau titik badan tiada kaitan dengan kelajuan. Vektor ini diarahkan ke arah perubahan kelajuan. Contohnya, untuk gerakan rectilinear, nilai a¯ boleh sama ada bertepatan dengan arah dengan v¯ atau bertentangan dengan v¯.
Paksa bertindak pada badan dan pecutan
Kami telah mendapati bahawa vektor pecutan jasad diarahkan ke arah perubahan vektor halaju. Walau bagaimanapun, tidak selalu mudah untuk menentukan bagaimana kelajuan berubah pada titik tertentu dalam trajektori. Selain itu, untuk menentukan perubahan dalam kelajuan, adalah perlu untuk melakukan operasiperbezaan vektor. Untuk mengelakkan kesukaran dalam menentukan arah vektor a¯, terdapat cara lain untuk mengetahui dengan cepat.
Di bawah ialah undang-undang Newton yang terkenal dan terkenal kepada setiap pelajar:
F¯=ma¯.
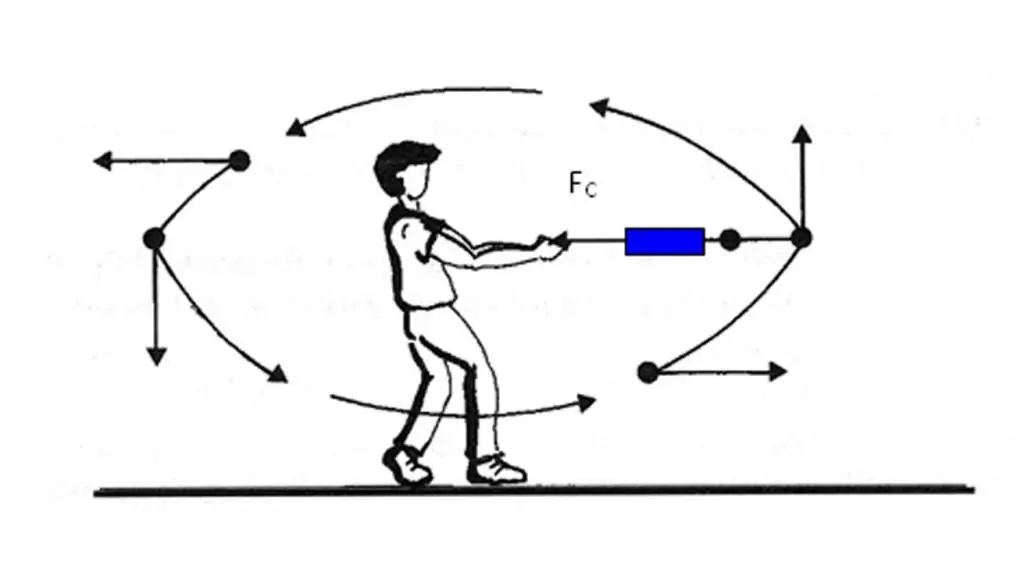
Formula menunjukkan bahawa punca pecutan dalam jasad adalah daya yang bertindak ke atasnya. Oleh kerana jisim m ialah skalar, vektor daya F dan vektor pecutan a berada dalam arah yang sama. Fakta ini harus diingat dan digunakan dalam amalan apabila terdapat keperluan untuk menentukan arah kuantiti a¯.
Jika beberapa daya berbeza bertindak ke atas badan, maka arah vektor pecutan akan sama dengan vektor yang terhasil bagi semua daya.
Gerakan bulat dan pecutan
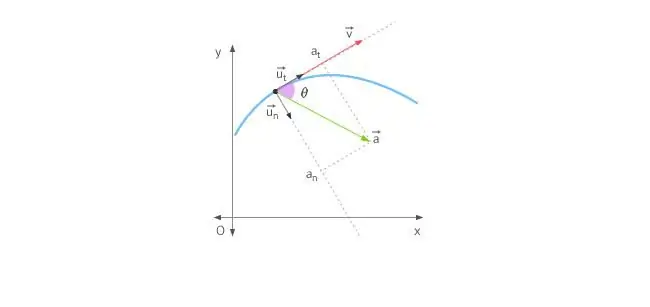
Apabila badan bergerak dalam garis lurus, pecutan diarahkan sama ada ke hadapan atau ke belakang. Dalam kes gerakan dalam bulatan, keadaan menjadi rumit oleh fakta bahawa vektor halaju sentiasa mengubah arahnya. Memandangkan perkara di atas, jumlah pecutan ditentukan oleh dua komponennya: tangen dan pecutan normal.
Pecutan tangensial diarahkan betul-betul sama dengan vektor halaju, atau menentangnya. Dalam erti kata lain, komponen pecutan ini diarahkan sepanjang tangen ke trajektori. Pecutan tangensial menerangkan perubahan dalam modulus kelajuan itu sendiri.
Pecutan biasa diarahkan sepanjang normal ke titik trajektori tertentu, dengan mengambil kira kelengkungannya. Dalam kes gerakan bulat, vektor komponen ini menunjukkanke pusat, iaitu, pecutan normal diarahkan sepanjang jejari putaran. Komponen ini selalunya dipanggil centripetal.
Pecutan penuh ialah jumlah komponen ini, jadi vektornya boleh diarahkan sewenang-wenangnya berkenaan dengan garis bulatan.
Jika jasad berputar tanpa mengubah halaju linear, maka hanya terdapat komponen normal bukan sifar, jadi vektor pecutan penuh dihalakan ke arah pusat bulatan. Ambil perhatian bahawa pusat ini juga dipengaruhi oleh daya yang mengekalkan badan pada trajektorinya. Contohnya, daya graviti Matahari mengekalkan Bumi dan planet-planet lain dalam orbitnya.






