Topik artikel kami hari ini ialah kinematik titik material. Apa itu semua? Apakah konsep yang terdapat di dalamnya dan apakah definisi yang harus diberikan kepada istilah ini? Kami akan cuba menjawab soalan ini dan banyak soalan lain hari ini.
Definisi dan konsep
Kinematik bagi titik material tidak lebih daripada subseksyen fizik yang dipanggil "mekanik". Dia pula mengkaji corak pergerakan badan-badan tertentu. Kinematik titik material juga menangani masalah ini, tetapi tidak melakukannya secara umum. Malah, subseksyen ini mengkaji kaedah yang membolehkan anda menerangkan pergerakan badan. Dalam kes ini, hanya badan yang dipanggil ideal yang sesuai untuk penyelidikan. Ini termasuk: titik material, jasad yang benar-benar tegar dan gas ideal. Mari kita pertimbangkan konsep dengan lebih terperinci. Kita semua tahu dari bangku sekolah bahawa adalah kebiasaan untuk memanggil titik material sebagai badan, dimensi yang dalam keadaan tertentu boleh diabaikan. Dengan cara ini, kinematik gerakan translasi titik material untuk kali pertama bermulaterdapat dalam buku teks fizik gred tujuh. Ini adalah cabang yang paling mudah, jadi paling mudah untuk mula berkenalan dengan sains dengan bantuannya. Soalan yang berasingan ialah apakah unsur-unsur kinematik titik material. Terdapat agak banyak daripada mereka, dan secara bersyarat mereka boleh dibahagikan kepada beberapa peringkat dengan kerumitan yang berbeza untuk pemahaman. Jika kita bercakap, sebagai contoh, mengenai vektor jejari, maka, pada dasarnya, tidak ada yang terlalu rumit dalam definisinya. Walau bagaimanapun, anda akan bersetuju bahawa lebih mudah untuk pelajar memahaminya berbanding pelajar sekolah menengah atau menengah. Dan sejujurnya, tidak perlu menerangkan ciri istilah ini kepada pelajar sekolah menengah.
Sejarah ringkas penciptaan kinematik
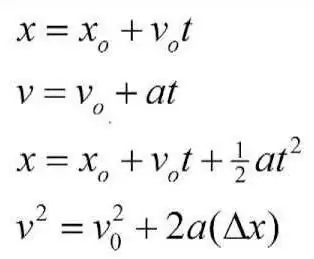
Banyak, bertahun-tahun yang lalu, saintis hebat Aristotle menumpukan sebahagian besar masa lapangnya kepada kajian dan penerangan fizik sebagai sains yang berasingan. Beliau juga bekerja pada kinematik, cuba membentangkan tesis dan konsep utamanya, satu cara atau yang lain digunakan dalam percubaan untuk menyelesaikan masalah praktikal dan juga setiap hari. Aristotle memberi idea awal tentang apakah unsur-unsur kinematik sesuatu titik material. Karya dan karya beliau sangat berharga untuk semua umat manusia. Namun begitu, dalam kesimpulannya dia membuat banyak kesilapan, dan sebabnya adalah salah tanggapan dan salah perhitungan tertentu. Pada satu masa, seorang saintis lain, Galileo Galilei, mula berminat dengan karya Aristotle. Salah satu tesis asas yang dikemukakan oleh Aristotle ialah pergerakan badanberlaku hanya jika ia digerakkan oleh beberapa daya, ditentukan oleh keamatan dan arah. Galileo membuktikan bahawa ini adalah satu kesilapan. Daya akan menjejaskan parameter kelajuan pergerakan, tetapi tidak lebih. Orang Itali menunjukkan bahawa daya adalah punca pecutan, dan ia hanya boleh timbul bersama dengannya. Juga, Galileo Galilei memberi perhatian yang besar kepada kajian proses jatuh bebas, memperoleh corak yang sesuai. Mungkin semua orang masih ingat eksperimen terkenalnya, yang dijalankannya di Menara Condong Pisa. Ahli fizik Ampère juga menggunakan asas penyelesaian kinematik dalam karyanya.
Konsep awal
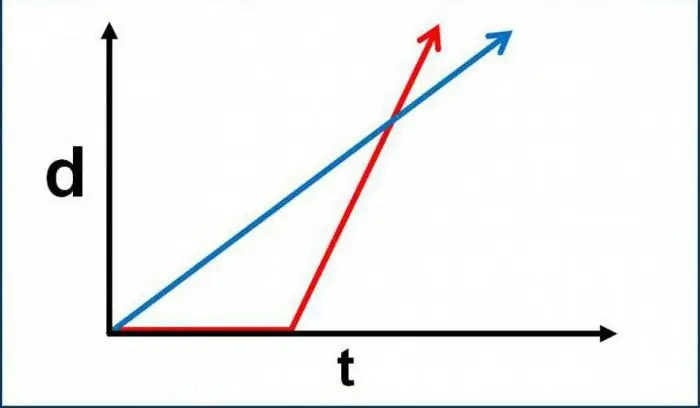
Seperti yang dinyatakan sebelum ini, kinematik ialah kajian tentang cara untuk menerangkan pergerakan objek yang ideal. Dalam kes ini, asas analisis matematik, algebra biasa dan geometri boleh digunakan dalam amalan. Tetapi apakah konsep (konsep tepat, dan bukan definisi untuk kuantiti parametrik) yang mendasari subseksyen fizik ini? Pertama, semua orang harus memahami dengan jelas bahawa kinematik gerakan translasi titik material menganggap gerakan tanpa mengambil kira penunjuk daya. Iaitu, untuk menyelesaikan masalah yang sepadan, kita tidak memerlukan formula yang berkaitan dengan daya. Ia tidak diambil kira oleh kinematik, tidak kira berapa banyak daripada mereka - satu, dua, tiga, sekurang-kurangnya beberapa ratus ribu. Namun begitu, kewujudan pecutan masih disediakan. Dalam beberapa masalah, kinematik pergerakan titik material menetapkan untuk menentukan magnitud pecutan. Walau bagaimanapun, punca fenomena ini (iaitu, daya dansifat mereka) tidak dianggap tetapi ditinggalkan.
Klasifikasi
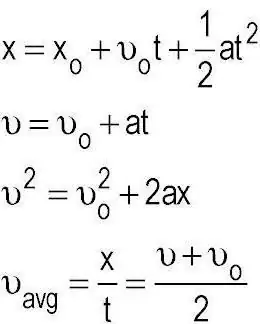
Kami mendapati bahawa kinematik meneroka dan menggunakan kaedah untuk menerangkan pergerakan jasad tanpa mengambil kira daya yang bertindak ke atasnya. Ngomong-ngomong, satu lagi subseksyen mekanik, yang dipanggil dinamik, menangani tugas sedemikian. Sudah ada, undang-undang Newton digunakan, yang membolehkan dalam amalan untuk menentukan cukup banyak parameter dengan sejumlah kecil data awal yang diketahui. Konsep asas kinematik titik material ialah ruang dan masa. Dan sehubungan dengan perkembangan sains secara am dan dalam bidang ini, timbul persoalan tentang kesesuaian penggunaan gabungan tersebut.
Sejak awal lagi terdapat kinematik klasik. Kita boleh mengatakan bahawa ia dicirikan bukan sahaja oleh kehadiran kedua-dua jurang temporal dan ruang, tetapi juga kebebasan mereka daripada pilihan satu atau lain kerangka rujukan. By the way, kita akan bercakap tentang ini sedikit kemudian. Sekarang mari kita jelaskan apa yang kita bincangkan. Dalam kes ini, segmen akan dianggap sebagai selang spatial, dan selang masa akan dianggap sebagai selang temporal. Semuanya nampak jelas. Jadi, jurang ini akan dipertimbangkan dalam kinematik klasik sebagai mutlak, invarian, dengan kata lain, bebas daripada peralihan daripada satu kerangka rujukan kepada yang lain. Sama ada kinematik relativistik perniagaan. Di dalamnya, jurang semasa peralihan antara sistem rujukan boleh berubah. Adalah lebih tepat untuk mengatakan bahawa mereka tidak boleh, tetapi mereka mesti, mungkin. Kerana ini, serentak kedua-duanyaperistiwa rawak juga menjadi relatif dan tertakluk kepada pertimbangan khusus. Itulah sebabnya dalam kinematik relativistik dua konsep - ruang dan masa - digabungkan menjadi satu.
Kinematik titik material: kelajuan, pecutan dan kuantiti lain
Untuk memahami sekurang-kurangnya sedikit bahagian fizik ini, anda perlu menavigasi konsep yang paling penting, mengetahui takrifan dan bayangkan apakah kuantiti ini atau itu secara umum. Tidak ada yang sukar dalam hal ini, malah semuanya sangat mudah dan ringkas. Pertimbangkan, mungkin, sebagai permulaan, konsep asas yang digunakan dalam masalah kinematik.
Pergerakan
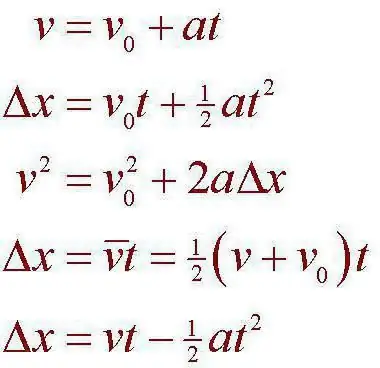
Pergerakan mekanikal kami akan mempertimbangkan proses semasa satu atau satu lagi objek ideal menukar kedudukannya di angkasa. Dalam kes ini, kita boleh mengatakan bahawa perubahan berlaku secara relatif kepada badan lain. Ia juga perlu mengambil kira hakikat bahawa penubuhan selang masa tertentu antara dua peristiwa berlaku serentak. Sebagai contoh, adalah mungkin untuk mengasingkan selang tertentu yang terbentuk semasa masa berlalu antara badan yang tiba dari satu kedudukan ke kedudukan yang lain. Kami juga ambil perhatian bahawa badan dalam kes ini boleh dan akan berinteraksi antara satu sama lain, mengikut undang-undang umum mekanik. Inilah yang paling kerap digunakan oleh kinematik titik material. Sistem rujukan ialah konsep seterusnya yang berkait rapat dengannya.
Koordinat
Ia boleh dipanggil data biasa yang membolehkan anda menentukan kedudukan badan pada satu masa atau yang lain. Koordinat berkait rapat dengan konsep sistem rujukan, serta grid koordinat. Selalunya ia adalah gabungan huruf dan nombor.
Vektor jejari
Daripada nama itu sepatutnya sudah jelas apa itu. Namun begitu, mari kita bincangkan perkara ini dengan lebih terperinci. Jika titik bergerak di sepanjang trajektori tertentu, dan kita tahu dengan tepat permulaan sistem rujukan tertentu, maka kita boleh melukis vektor jejari pada bila-bila masa. Ia akan menyambungkan kedudukan awal titik ke kedudukan serta-merta atau akhir.
Trajektori
Ia akan dipanggil garis berterusan, yang diletakkan hasil daripada pergerakan titik material dalam sistem rujukan tertentu.
Kelajuan (kedua-dua linear dan sudut)
Ini ialah nilai yang boleh memberitahu berapa cepat badan melalui selang jarak tertentu.
Pecutan (kedua-dua sudut dan linear)
Menunjukkan mengikut undang-undang dan seberapa intensif parameter kelajuan badan berubah.
Mungkin, inilah mereka - elemen utama kinematik titik material. Perlu diingatkan bahawa kedua-dua halaju dan pecutan adalah kuantiti vektor. Dan ini bermakna bahawa mereka bukan sahaja mempunyai beberapa nilai indikatif, tetapi juga arah tertentu. Ngomong-ngomong, mereka boleh diarahkan kedua-duanya dalam satu arah dan dalam arah yang bertentangan. Dalam kes pertama, badan akan memecut, dalam kes kedua ia akan perlahan.
Tugas mudah
Kinematik bagi titik material (halaju, pecutan dan jarak yang merupakan konsep asas secara praktikal) merangkumi bukan sahaja sejumlah besar tugas, tetapi banyak kategorinya yang berbeza. Mari cuba selesaikan masalah yang agak mudah dengan menentukan jarak yang dilalui oleh badan.
Andaikan syarat yang kami ada adalah seperti berikut. Kereta pemandu berada di garisan permulaan. Pengendali memberi kebenaran dengan bendera, dan kereta itu berlepas secara tiba-tiba. Tentukan sama ada dia boleh mencipta rekod baru dalam pertandingan pelumba, jika pendahulu seterusnya menempuh jarak seratus meter dalam 7.8 saat. Ambil pecutan kereta bersamaan dengan 3 meter dibahagikan dengan kuasa dua kedua.
Jadi, bagaimana untuk menyelesaikan masalah ini? Ia agak menarik, kerana kita dikehendaki untuk tidak "kering" menentukan parameter tertentu. Ia diserikan dengan pusing ganti dan situasi tertentu, yang mempelbagaikan proses penyelesaian dan mencari petunjuk. Tetapi apakah yang harus kita pandu sebelum menghampiri tugas?
1. Kinematik titik material menyediakan penggunaan pecutan dalam kes ini.
2. Penyelesaian diandaikan menggunakan formula jarak, kerana nilai berangkanya muncul dalam keadaan.
Masalah ini sebenarnya diselesaikan dengan mudah. Untuk melakukan ini, kami mengambil formula jarak: S=VoT + (-) AT ^ 2/2. Apa gunanya? Kita perlu mengetahui berapa lama penunggang akan menempuh jarak yang ditetapkan, dan kemudian membandingkan angka itu dengan rekod untuk mengetahui sama ada dia mengalahkannya atau tidak. Untuk melakukan ini, peruntukkan masa, kami memperoleh formulauntuknya: AT^2 + 2VoT - 2S. Ini tidak lebih daripada persamaan kuadratik. Tetapi kereta itu berlepas, yang bermaksud bahawa kelajuan awal akan menjadi 0. Apabila menyelesaikan persamaan, diskriminasi akan sama dengan 2400. Untuk mencari masa, anda perlu mengambil akarnya. Mari kita lakukannya ke tempat perpuluhan kedua: 48.98. Cari punca persamaan: 48.98/6=8.16 saat. Ternyata pemandu tidak akan dapat mengatasi rekod sedia ada.






