Hukum Ohm ialah hukum asas litar elektrik. Pada masa yang sama, ia membolehkan kita menerangkan banyak fenomena alam. Sebagai contoh, seseorang boleh memahami mengapa elektrik tidak "menewaskan" burung yang duduk di atas wayar. Bagi fizik, undang-undang Ohm adalah sangat penting. Tanpa pengetahuan beliau, adalah mustahil untuk mencipta litar elektrik yang stabil atau tidak akan wujud sama sekali elektronik.
Pergantungan I=I(U) dan nilainya
Sejarah penemuan rintangan bahan secara langsung berkaitan dengan ciri voltan semasa. Apa ini? Mari kita ambil litar dengan arus elektrik yang berterusan dan pertimbangkan mana-mana elemennya: lampu, paip gas, konduktor logam, kelalang elektrolit, dsb.
Menukar voltan U (sering dirujuk sebagai V) yang dibekalkan kepada elemen yang dimaksudkan, kami akan menjejaki perubahan kekuatan arus (I) yang melaluinya. Akibatnya, kita akan mendapat pergantungan bentuk I \u003d I (U), yang dipanggil "ciri voltan elemen" dan merupakan penunjuk langsung baginya.sifat elektrik.
V/A ciri mungkin kelihatan berbeza untuk elemen yang berbeza. Bentuknya yang paling mudah diperoleh dengan mempertimbangkan konduktor logam, yang dilakukan oleh Georg Ohm (1789 - 1854).
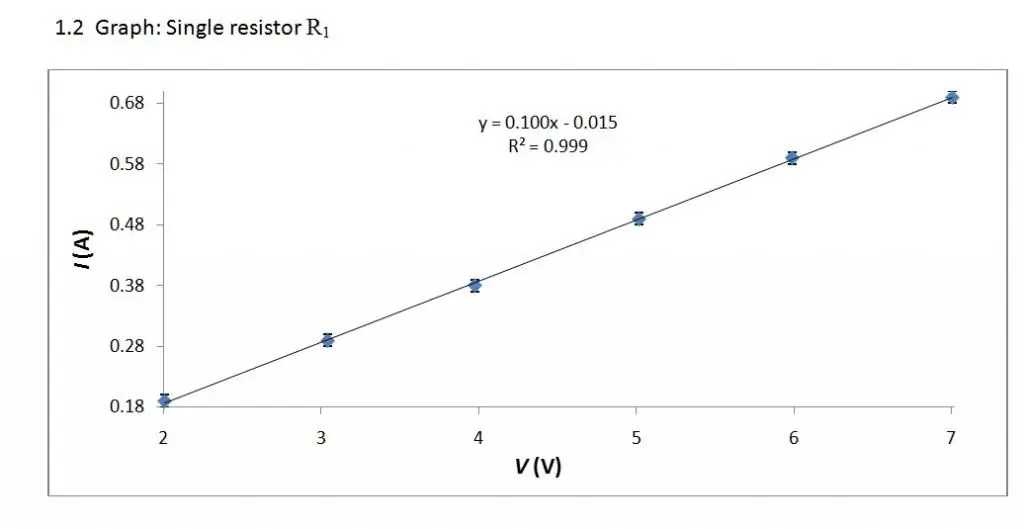
Ciri volt-ampere ialah hubungan linear. Oleh itu, grafnya ialah garis lurus.
Undang-undang dalam bentuk paling mudah
Penyelidikan Ohm tentang ciri voltan arus konduktor menunjukkan bahawa kekuatan arus di dalam konduktor logam adalah berkadar dengan beza keupayaan pada hujungnya (I ~ U) dan berkadar songsang dengan pekali tertentu, iaitu, I ~ 1/R. Pekali ini dikenali sebagai "rintangan konduktor", dan unit ukuran rintangan elektrik ialah Ohm atau V/A.
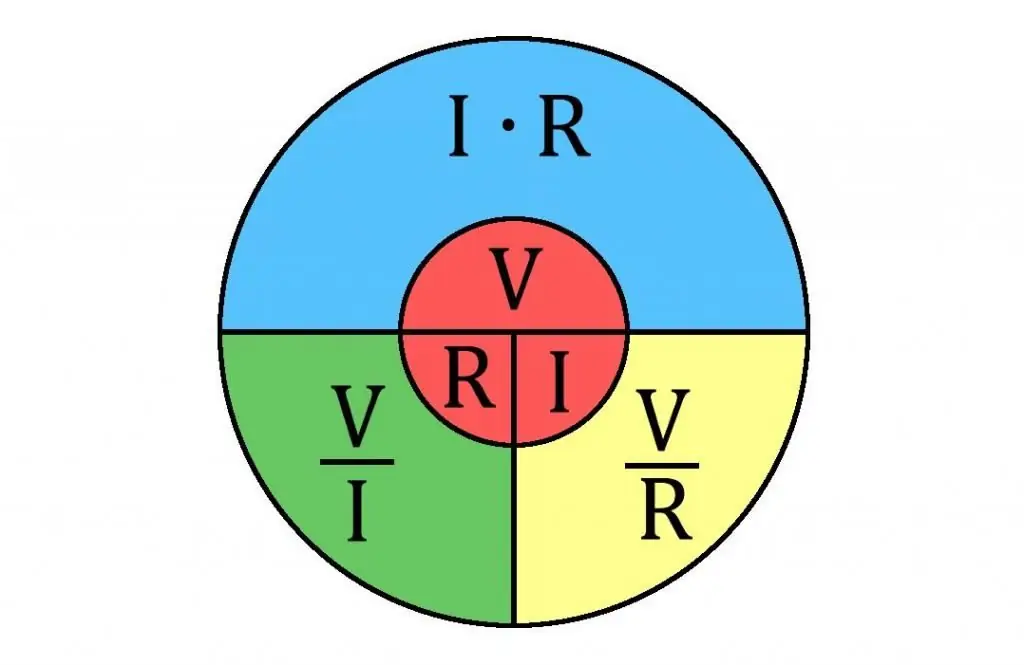
Satu lagi perkara yang perlu diperhatikan. Hukum Ohm sering digunakan untuk mengira rintangan dalam litar.
Perkataan undang-undang
Hukum Ohm mengatakan bahawa kekuatan arus (I) bagi satu bahagian litar adalah berkadar dengan voltan dalam bahagian ini dan berkadar songsang dengan rintangannya.
Perlu diingatkan bahawa dalam bentuk ini hukum tetap berlaku hanya untuk bahagian rantai yang homogen. Homogen ialah bahagian litar elektrik yang tidak mengandungi sumber arus. Cara menggunakan hukum Ohm dalam litar tak homogen akan dibincangkan di bawah.
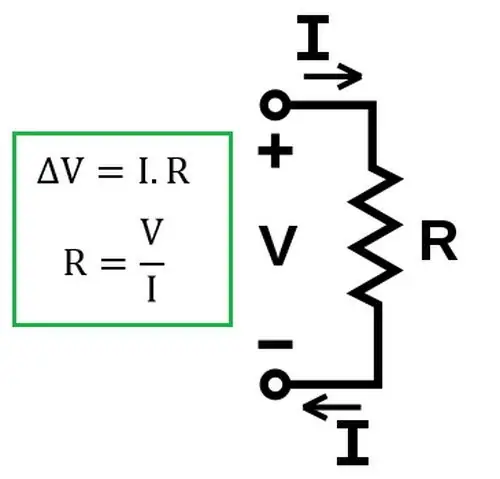
Kemudian, didapati secara eksperimen bahawa undang-undang tetap sah untuk penyelesaianelektrolit dalam litar elektrik.
Makna fizikal rintangan
Rintangan ialah sifat bahan, bahan atau media untuk menghalang laluan arus elektrik. Secara kuantitatif, rintangan 1 ohm bermakna bahawa dalam konduktor dengan voltan 1 V pada hujungnya, arus elektrik 1 A boleh melalui.
Kerintangan elektrik
Secara eksperimen, didapati rintangan arus elektrik konduktor bergantung pada dimensinya: panjang, lebar, tinggi. Dan juga pada bentuknya (sfera, silinder) dan bahan dari mana ia dibuat. Oleh itu, formula untuk kerintangan, sebagai contoh, konduktor silinder homogen ialah: R \u003d pl / S.
Jika dalam formula ini kita meletakkan s=1 m2 dan l=1 m, maka R secara berangka akan sama dengan p. Dari sini, unit ukuran untuk pekali kerintangan konduktor dalam SI dikira - ini ialah Ohmm.

Dalam formula kerintangan, p ialah pekali rintangan yang ditentukan oleh sifat kimia bahan dari mana konduktor dibuat.
Untuk mempertimbangkan bentuk pembezaan hukum Ohm, kita perlu mempertimbangkan beberapa konsep lagi.
Ketumpatan semasa
Seperti yang anda ketahui, arus elektrik ialah pergerakan tertib bagi mana-mana zarah bercas. Contohnya, dalam logam, pembawa arus ialah elektron, dan dalam pengaliran gas, ion.
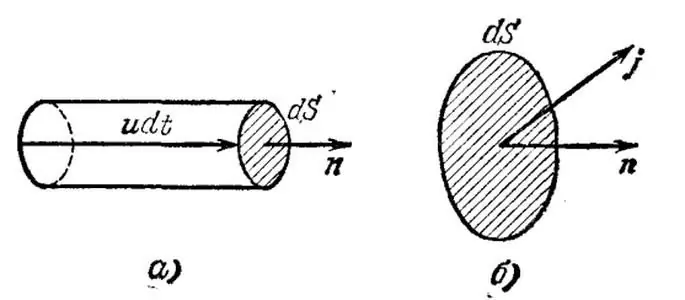
Ambil kes remeh apabila semua pembawa semasahomogen - konduktor logam. Marilah kita secara mental memilih isipadu tak terhingga kecil dalam konduktor ini dan menandakan dengan u halaju purata (hanyut, tertib) elektron dalam isipadu yang diberikan. Selanjutnya, biarkan n menyatakan kepekatan pembawa semasa per unit volum.
Sekarang mari kita lukiskan luas tak terhingga dS berserenjang dengan vektor u dan bina sepanjang halaju sebuah silinder tak terhingga dengan ketinggian udt, di mana dt menandakan masa di mana semua pembawa halaju semasa yang terkandung dalam isipadu yang dipertimbangkan akan berlalu. melalui kawasan dS.
Dalam kes ini, cas bersamaan dengan q=neudSdt akan dipindahkan oleh elektron melalui kawasan, di mana e ialah cas elektron. Oleh itu, ketumpatan arus elektrik ialah vektor j=neu, menandakan jumlah cas yang dipindahkan setiap unit masa melalui satu unit luas.
Salah satu faedah definisi pembezaan Hukum Ohm ialah anda selalunya boleh bertahan tanpa mengira rintangan.
Caj elektrik. Kekuatan medan elektrik
Kekuatan medan bersama-sama dengan cas elektrik ialah parameter asas dalam teori elektrik. Pada masa yang sama, idea kuantitatif tentang mereka boleh diperoleh daripada eksperimen mudah yang tersedia untuk pelajar sekolah.
Untuk memudahkan, kami akan mempertimbangkan medan elektrostatik. Ini adalah medan elektrik yang tidak berubah mengikut masa. Medan sedemikian boleh dicipta dengan cas elektrik pegun.
Selain itu, caj ujian diperlukan untuk tujuan kami. Dalam kapasitinya kami akan menggunakan badan bercas - sangat kecil sehingga tidak mampu menyebabkannyasebarang gangguan (pengagihan semula caj) dalam objek sekeliling.
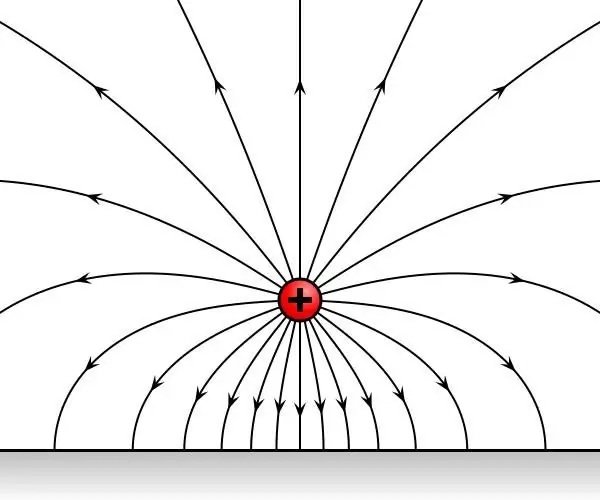
Mari kita pertimbangkan pula dua caj ujian yang diambil, diletakkan berturut-turut pada satu titik di angkasa, yang berada di bawah pengaruh medan elektrostatik. Ternyata pertuduhan itu akan tertakluk kepada pengaruh invariant masa di pihaknya. Biarkan F1 dan F2 menjadi kuasa yang bertindak ke atas tuduhan.
Hasil daripada generalisasi data eksperimen, didapati bahawa daya F1 dan F2 diarahkan sama ada dalam satu atau dalam arah yang bertentangan, dan nisbahnya F1/F2 adalah bebas daripada titik dalam ruang di mana caj ujian diletakkan secara bergilir-gilir. Oleh itu, nisbah F1/F2 ialah ciri caj itu sendiri dan tidak bergantung pada medan.
Penemuan fakta ini memungkinkan untuk mencirikan elektrisasi badan dan kemudiannya dipanggil cas elektrik. Oleh itu, mengikut definisi, ternyata q1/q2=F1/F 2 , dengan q1 dan q2 - jumlah caj yang diletakkan pada satu titik medan dan F 1 dan F2 - memaksa bertindak atas tuduhan dari sisi medan.
Daripada pertimbangan sedemikian, magnitud cas pelbagai zarah telah ditentukan secara eksperimen. Dengan menetapkan secara bersyarat salah satu caj ujian sama dengan satu dalam nisbah, anda boleh mengira nilai caj yang lain dengan mengukur nisbah F1/F2.
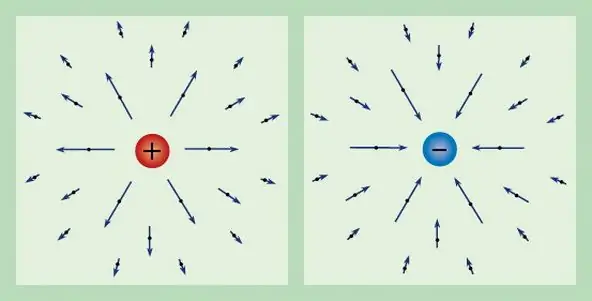
Sebarang medan elektrik boleh dicirikan melalui cas yang diketahui. Oleh itu, daya yang bertindak pada cas ujian unit pada keadaan pegun dipanggil kekuatan medan elektrik dan dilambangkan dengan E. Daripada takrifan cas, kita memperoleh bahawa vektor kekuatan mempunyai bentuk berikut: E=F/q.
Sambungan vektor j dan E. Satu lagi bentuk hukum Ohm
Dalam konduktor homogen, pergerakan tertib zarah bercas akan berlaku ke arah vektor E. Ini bermakna vektor j dan E akan diarahkan bersama. Seperti dalam menentukan ketumpatan semasa, kami memilih isipadu silinder yang sangat kecil dalam konduktor. Kemudian arus bersamaan dengan jdS akan melalui keratan rentas silinder ini, dan voltan yang dikenakan pada silinder akan sama dengan Edl. Formula untuk kerintangan silinder juga diketahui.
Kemudian, menulis formula untuk kekuatan semasa dalam dua cara, kita dapat: j=E/p, di mana nilai 1/p dipanggil kekonduksian elektrik dan merupakan songsangan bagi kerintangan elektrik. Ia biasanya dilambangkan σ (sigma) atau λ (lambda). Unit kekonduksian ialah Sm/m, di mana Sm ialah Siemens. Unit songsang bagi Ohm.
Oleh itu, kita boleh menjawab soalan yang dikemukakan di atas tentang hukum Ohm untuk litar tidak homogen. Dalam kes ini, pembawa semasa akan dipengaruhi oleh daya dari medan elektrostatik, yang dicirikan oleh keamatan E1, dan daya lain yang bertindak ke atasnya daripada sumber arus lain, yang boleh ditetapkan E 2. Kemudian Hukum Ohm digunakan untukbahagian rantai yang tidak homogen akan kelihatan seperti: j=λ(E1 + E2).
Lebih lanjut tentang Kekonduksian dan Rintangan
Keupayaan konduktor untuk mengalirkan arus elektrik dicirikan oleh kerintangannya, yang boleh didapati melalui formula kerintangan, atau kekonduksian, dikira sebagai timbal balik kekonduksian. Nilai parameter ini ditentukan oleh sifat kimia bahan konduktor dan oleh keadaan luaran. Khususnya, suhu ambien.
Bagi kebanyakan logam, kerintangan pada suhu normal adalah berkadar dengannya, iaitu, p ~ T. Walau bagaimanapun, sisihan diperhatikan pada suhu rendah. Untuk sejumlah besar logam dan aloi pada suhu hampir 0°K, pengiraan rintangan menunjukkan nilai sifar. Fenomena ini dipanggil superkonduktiviti. Contohnya, merkuri, timah, plumbum, aluminium, dll. mempunyai sifat ini. Setiap logam mempunyai suhu kritikalnya sendiri Tk, di mana fenomena superkonduktiviti diperhatikan.
Juga ambil perhatian bahawa takrifan kerintangan silinder boleh digeneralisasikan kepada wayar yang diperbuat daripada bahan yang sama. Dalam kes ini, luas keratan rentas daripada formula kerintangan akan sama dengan keratan rentas wayar, dan l - panjangnya.






