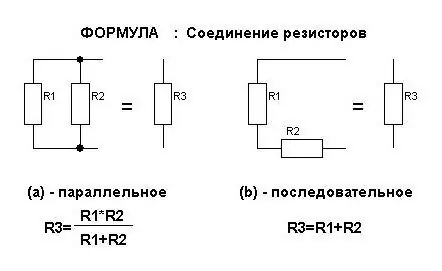
Dalam fizik, topik sambungan selari dan siri dikaji, dan ia bukan sahaja konduktor, tetapi juga kapasitor. Adalah penting di sini untuk tidak keliru tentang bagaimana setiap daripada mereka kelihatan pada rajah. Dan hanya kemudian gunakan formula khusus. By the way, anda perlu mengingati mereka dengan hati.
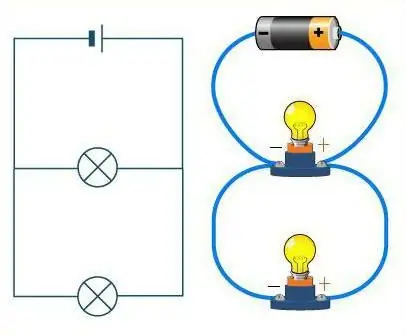
Bagaimana untuk membezakan antara dua sebatian ini?
Lihat gambar rajah dengan teliti. Jika wayar diwakili sebagai jalan, maka kereta di atasnya akan memainkan peranan perintang. Di jalan lurus tanpa sebarang persimpangan, kereta memandu satu demi satu, dalam rantai. Sambungan siri konduktor juga kelihatan sama. Jalan dalam kes ini boleh mempunyai bilangan selekoh yang tidak terhad, tetapi bukan satu persimpangan. Tidak kira bagaimana jalan (wayar) bergoyang, mesin (perintang) akan sentiasa terletak satu demi satu, dalam satu rantai.
Perkara yang agak berbeza jika sambungan selari dipertimbangkan. Kemudian perintang boleh dibandingkan dengan atlet pada permulaan. Mereka adalahmasing-masing berdiri di landasan sendiri, tetapi mereka mempunyai arah pergerakan yang sama, dan garisan penamat berada di tempat yang sama. Begitu juga, perintang - setiap daripadanya mempunyai wayar sendiri, tetapi semuanya disambungkan pada satu ketika.
Formula untuk kekuatan semasa
Ia sentiasa dibincangkan dalam topik "Elektrik". Sambungan selari dan siri mempengaruhi jumlah arus dalam perintang dengan cara yang berbeza. Bagi mereka, formula terhasil yang boleh diingati. Tetapi cukup sekadar mengingati makna yang dilaburkan dalam diri mereka.
Jadi, arus dalam sambungan bersiri konduktor sentiasa sama. Iaitu, dalam setiap daripada mereka nilai kekuatan semasa tidak berbeza. Anda boleh melukis analogi jika anda membandingkan wayar dengan paip. Di dalamnya, air sentiasa mengalir dengan cara yang sama. Dan semua halangan di laluannya akan dihanyutkan dengan kekuatan yang sama. Sama dengan semasa. Oleh itu, formula untuk jumlah arus dalam litar dengan sambungan siri perintang kelihatan seperti ini:
Saya gen=Saya 1=Saya 2
Di sini, huruf I menandakan kekuatan arus. Ini ialah notasi biasa, jadi anda perlu mengingatinya.
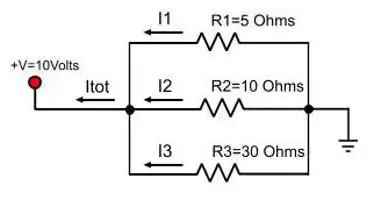
Arus dalam sambungan selari tidak lagi menjadi nilai tetap. Dengan analogi yang sama dengan paip, ternyata air akan terbahagi kepada dua aliran jika paip utama mempunyai cabang. Fenomena yang sama diperhatikan dengan arus apabila cawangan wayar muncul di laluannya. Formula untuk jumlah kekuatan arus apabila konduktor disambung secara selari:
I gen=I 1 + I 2
Jika dahan itu terdiri daripada wayar itulebih daripada dua, maka dalam formula di atas akan terdapat lebih banyak sebutan dengan nombor yang sama.
Formula untuk tekanan
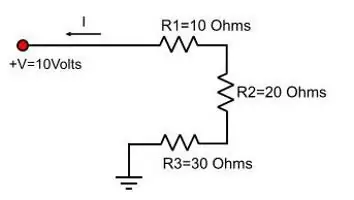
Apabila litar dipertimbangkan di mana konduktor disambungkan secara bersiri, voltan dalam keseluruhan bahagian ditentukan oleh jumlah nilai ini pada setiap perintang tertentu. Anda boleh membandingkan keadaan ini dengan plat. Ia akan menjadi mudah bagi seseorang untuk memegang salah satu daripada mereka, dia juga akan dapat mengambil yang kedua berdekatan, tetapi dengan kesukaran. Seseorang tidak lagi dapat memegang tiga pinggan bersebelahan, bantuan sesaat akan diperlukan. Dan lain-lain. Usaha orang ramai bertambah.
Formula untuk jumlah voltan bahagian litar dengan sambungan siri konduktor kelihatan seperti ini:
U gen=U 1 + U 2, di mana U ialah sebutan yang diterima pakai untuk voltan elektrik.
Situasi lain timbul jika sambungan selari perintang dipertimbangkan. Apabila pinggan disusun di atas satu sama lain, ia masih boleh dipegang oleh seorang. Jadi anda tidak perlu menambah apa-apa. Analogi yang sama diperhatikan apabila konduktor disambung secara selari. Voltan pada setiap daripadanya adalah sama dan sama dengan yang ada pada kesemuanya sekaligus. Formula untuk jumlah voltan ialah:
U gen=U 1=U 2
Formula untuk rintangan elektrik
Anda tidak boleh lagi menghafalnya, tetapi ketahui formula hukum Ohm dan dapatkan yang dikehendaki daripadanya. Ia berikutan daripada undang-undang ini bahawavoltan adalah sama dengan hasil darab arus dan rintangan. Iaitu, U=IR, dengan R ialah rintangan.
Maka formula yang perlu anda gunakan bergantung pada cara konduktor disambungkan:
- dalam siri, jadi anda memerlukan kesamaan untuk voltan - IgenRjumlah=I1R1 + I2R2;
- secara selari, perlu menggunakan formula untuk kekuatan semasa - Ujumlah / Rjumlah=U 1/ R1 + U2 / R2 .
Diikuti dengan transformasi mudah, yang berdasarkan fakta bahawa dalam kesamaan pertama semua arus mempunyai nilai yang sama, dan pada yang kedua - voltan adalah sama. Jadi mereka boleh dipendekkan. Iaitu, ungkapan berikut diperoleh:
- R gen=R 1 + R 2 (untuk sambungan siri konduktor).
- 1 / R gen=1 / R 1 + 1 / R 2(apabila disambung secara selari).
Apabila bilangan perintang yang disambungkan ke rangkaian bertambah, bilangan sebutan dalam ungkapan ini berubah.
Perlu diperhatikan bahawa sambungan selari dan siri konduktor mempunyai kesan yang berbeza pada jumlah rintangan. Yang pertama mengurangkan rintangan bahagian litar. Lebih-lebih lagi, ia ternyata kurang daripada perintang terkecil yang digunakan. Apabila disambungkan secara bersiri, semuanya adalah logik: nilai tambah, jadi jumlah bilangan akan sentiasa terbesar.
Kerja semasa
Tiga kuantiti sebelumnya membentuk hukum sambungan selari dan susunan siri konduktor dalam litar. Oleh itu, adalah penting untuk mengenali mereka. Mengenai kerja dan kuasa, anda hanya perlu ingat formula asas. Ia ditulis seperti berikut: A \u003d IUt, di mana A ialah kerja arus, t ialah masa laluannya melalui konduktor.
Untuk menentukan jumlah kerja dengan sambungan bersiri, anda perlu menggantikan voltan dalam ungkapan asal. Anda mendapat kesamaan: A \u003d I(U 1 + U 2)t, membuka kurungan yang ternyata kerja pada keseluruhan bahagian adalah sama dengan jumlah mereka pada setiap pengguna semasa tertentu.
Penalaran diteruskan dengan cara yang sama jika skema sambungan selari dipertimbangkan. Hanya kekuatan semasa yang sepatutnya diganti. Tetapi hasilnya akan sama: A=A 1 + A 2.
Kuasa semasa
Apabila memperoleh formula untuk kuasa (notasi "P") bahagian litar, anda sekali lagi perlu menggunakan satu formula: P \u003d UI. Selepas penalaran sedemikian, ternyata sambungan selari dan siri adalah diterangkan oleh formula kuasa sedemikian: P \u003d P1 + P 2.
Iaitu, tidak kira bagaimana skema itu disusun, jumlah kuasa adalah jumlah mereka yang terlibat dalam kerja. Ini menjelaskan hakikat bahawa adalah mustahil untuk memasukkan banyak peranti berkuasa dalam rangkaian apartmen pada masa yang sama. Dia tidak boleh menanggung beban.
Bagaimanakah sambungan konduktor mempengaruhi pembaikan kalungan Tahun Baru?
Sejurus selepas salah satu mentol terbakar, ia menjadi jelas bagaimana ia disambungkan. Padasambungan bersiri, tiada satu pun daripada mereka akan menyala. Ini disebabkan oleh fakta bahawa lampu yang telah menjadi tidak boleh digunakan mencipta rehat dalam litar. Oleh itu, anda perlu menyemak segala-galanya untuk menentukan yang mana yang hangus, gantikannya - dan kalungan akan mula berfungsi.
Jika ia menggunakan sambungan selari, ia tidak akan berhenti berfungsi jika salah satu mentol gagal. Lagipun, rantai itu tidak akan putus sepenuhnya, tetapi hanya satu bahagian selari. Untuk membaiki kalungan sedemikian, anda tidak perlu menyemak semua elemen litar, tetapi hanya elemen yang tidak bercahaya.
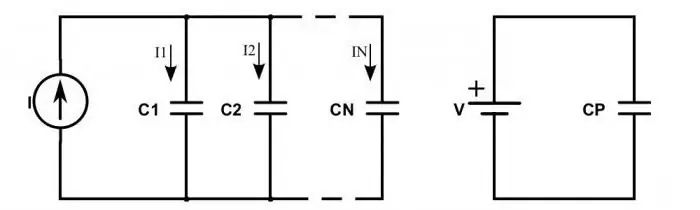
Apakah yang berlaku kepada litar jika kapasitor disertakan dan bukannya perintang?
Apabila ia disambungkan secara bersiri, situasi berikut diperhatikan: caj daripada tambah sumber kuasa hanya datang ke plat luar kapasitor ekstrem. Mereka yang berada di antara hanya meneruskan caj itu di sepanjang rantai. Ini menjelaskan fakta bahawa caj yang sama muncul pada semua plat, tetapi dengan tanda yang berbeza. Oleh itu, cas elektrik setiap kapasitor yang disambungkan secara bersiri boleh ditulis seperti berikut:
q gen =q 1=q 2.
Untuk menentukan voltan pada setiap kapasitor, anda perlu mengetahui formula: U=q / C. Di dalamnya, C ialah kemuatan kapasitor.
Jumlah voltan mengikut undang-undang yang sama seperti perintang. Oleh itu, menggantikan voltan dalam formula kemuatan dengan jumlah, kita mendapat bahawa jumlah kapasitansi peranti mesti dikira menggunakan formula:
C=q / (U 1 + U2).
Anda boleh memudahkan formula ini dengan membalikkan pecahan dan menggantikan nisbah voltan untuk mengecas dengan kapasitansi. Ternyata persamaan berikut: 1 / С=1 / С 1 + 1 / С 2.
Keadaan kelihatan agak berbeza apabila kapasitor disambung secara selari. Kemudian jumlah caj ditentukan oleh jumlah semua caj yang terkumpul pada plat semua peranti. Dan nilai voltan masih ditentukan mengikut undang-undang am. Oleh itu, formula untuk jumlah kapasiti kapasitor yang disambung secara selari ialah:
С=(q 1 + q 2) / U.
Iaitu, nilai ini dianggap sebagai jumlah setiap peranti yang digunakan dalam sambungan:
S=S 1 + S 2.
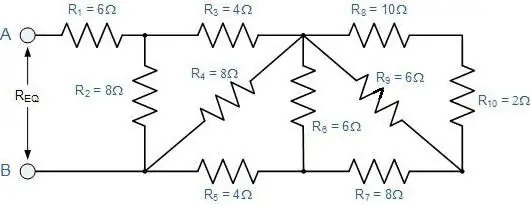
Bagaimana untuk menentukan jumlah rintangan sambungan sewenang-wenangnya konduktor?
Iaitu, bahagian di mana bahagian berturut-turut menggantikan yang selari, dan sebaliknya. Bagi mereka, semua undang-undang yang diterangkan masih sah. Hanya anda perlu menerapkannya secara berperingkat.
Pertama, ia sepatutnya mengembangkan skema secara mental. Sekiranya sukar untuk membayangkannya, maka anda perlu melukis apa yang berlaku. Penjelasan akan menjadi lebih jelas jika kita mempertimbangkannya dengan contoh khusus (lihat rajah).
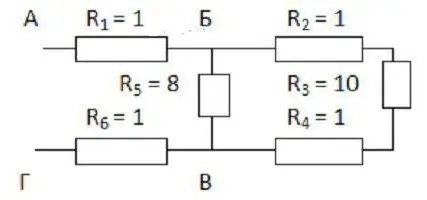
Adalah mudah untuk mula melukis dari titik B dan C. Ia mesti diletakkan pada jarak yang agak jauh antara satu sama lain dan dari tepi helaian. Di sebelah kiri, satu wayar menghampiri titik B, dan dua sudah diarahkan ke kanan. Titik B pula, mempunyai dua cabang di sebelah kiri dan satu wayar selepasnya.
Kini anda perlu mengisi ruang di antara inititik. Tiga perintang dengan pekali 2, 3 dan 4 harus diletakkan di sepanjang wayar atas, dan yang dengan indeks 5 akan pergi dari bawah. Tiga yang pertama disambungkan secara bersiri. Dengan perintang kelima mereka selari.
Baki dua perintang (yang pertama dan keenam) disambungkan secara bersiri dengan bahagian BV yang dipertimbangkan. Oleh itu, lukisan hanya boleh ditambah dengan dua segi empat tepat pada kedua-dua belah mata yang dipilih. Ia kekal menggunakan formula untuk mengira rintangan:
- pertama yang diberikan untuk sambungan bersiri;
- kemudian untuk selari;
- dan sekali lagi untuk berturut-turut.
Dengan cara ini, anda boleh menggunakan mana-mana, malah skim yang sangat kompleks.
Masalah sambungan bersiri konduktor
Keadaan. Dua lampu dan perintang disambungkan dalam litar satu di belakang yang lain. Jumlah voltan ialah 110 V dan arus ialah 12 A. Berapakah nilai perintang jika setiap lampu berkadar pada 40 V?
Keputusan. Oleh kerana sambungan siri sedang dipertimbangkan, formula untuk undang-undangnya diketahui. Anda hanya perlu mengaplikasikannya dengan betul. Mulakan dengan mengetahui nilai voltan merentasi perintang. Untuk melakukan ini, anda perlu menolak dua kali voltan satu lampu daripada jumlah keseluruhan. Ternyata 30 V.
Sekarang dua kuantiti diketahui, U dan I (yang kedua diberikan dalam keadaan, kerana jumlah arus adalah sama dengan arus dalam setiap pengguna siri), kita boleh mengira rintangan perintang menggunakan Hukum Ohm. Ternyata 2.5 ohm.
Jawapan. Rintangan perintang ialah 2.5 ohm.
Tugasuntuk sambungan kapasitor, selari dan siri
Keadaan. Terdapat tiga kapasitor dengan kapasiti 20, 25 dan 30 mikrofarad. Tentukan jumlah kapasitansi apabila disambung secara bersiri dan selari.
Keputusan. Lebih mudah untuk bermula dengan sambungan selari. Dalam keadaan ini, ketiga-tiga nilai hanya perlu ditambah. Oleh itu, jumlah kapasiti ialah 75uF.
Pengiraan akan menjadi lebih rumit apabila kapasitor ini disambungkan secara bersiri. Lagipun, pertama anda perlu mencari nisbah perpaduan kepada setiap kapasiti ini, dan kemudian menambahnya antara satu sama lain. Ternyata unit dibahagikan dengan jumlah kapasiti ialah 37/300. Maka nilai yang dikehendaki ialah lebih kurang 8 mikrofarad.
Jawapan. Jumlah kapasiti dalam sambungan bersiri ialah 8 uF, selari - 75 uF.






